(二)受弯构件挠度的验算
1.挠度与刚度
在材料力学对匀质材料梁的变形计算中,给出了简支梁在均布荷载q作用下的跨中挠度为:

式中 f——梁的跨中最大挠度;
M——跨中最大弯矩;
β—挠度系数,与荷载形式及支承条件有关;
EI——梁的截面抗弯刚度;
l一梁的计算跨度。
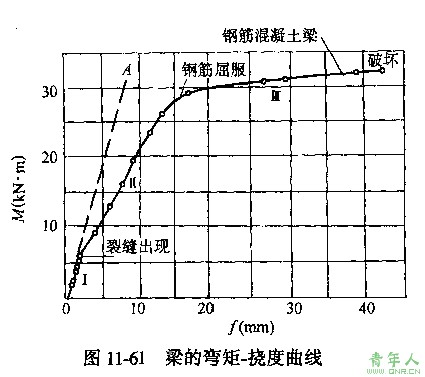
从式(11—142)中可以看出,对于匀质弹性材料梁,当梁的截面尺寸、材料一定时EI为常数,其弯矩—挠度(M—f)呈线性关系,如图11-61中O-A虚线所示。而钢筋混凝土构件则不同,其实测的M-f曲线表明,只有在荷载很小梁尚未开裂时(阶段1),M-f线才是一段直线,从开始出现裂缝到钢筋屈服时(阶段Ⅱ),M-f线开始偏离直线而逐渐向下弯曲,这说明构件刚度开始下降。但这时梁仍处于正常使用阶段。当继续加载时,受拉钢筋屈服(阶段Ⅲ),M-f线更偏向横轴(f轴),挠度值增长更快。上述现象说明,钢筋混凝土梁的刚度不是一个常数,而是随着荷载的增加而降低。从而,计算其变形问题就归结为计算它的抗弯问题了。梁的抗弯刚度也就分成短期刚度和长期刚度两种:短期刚度Bs表示在荷载短期效应作用下受弯构件截面的抗弯刚度;长期刚度B表示考虑了一部分荷载长期作用影响后截面的抗弯刚度。
责任编辑:xiaohan

