四、回归分析
1、回归分析的意义回归分析是对具有相关关系的两个或/考*试*大/两个以上变量之间数量变化的一般关系进行测定,确定一个相应的数学表达式,以便从一个已知量来推测另一个未知量,为估计预测提供一个重要的方法。
2、回归与相关的区别与联系回归和相关都是研究两个变量相互关系的分析方法。相关分析研究两个变量之间相关的方向和相关的密切程度。但是相关分析不能指出两变量相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化关系。回归方程则是通过一定的数学方程来反映变量之间相互关系的具体形式,以便从一个已知量来推测另一个未知量。为估算预测提供一个重要的方法。
计算相关系数的两变量是对等的,可以都是随机变量,各自接受随机因素的影响,改变两变量的地位并不影响相关系数的数值。在回归分析中因变量是随机的,自变量是可控制的解释变量,不是随机变量。因此回归分析只能用自变量来估计因变量,而不允许由因变量来推测自变量。
回归分析和相关分析是互相补充、密切联系的。相关分析需要回归分析来表明现象数量相关的具体形式,而回归分析则应该建立在相关分析的基础上。依靠相关分析表明现象的数量变化具有密切相关,进行回归分析求其相关的具体形式才有意义。在相关程度很低的情况下,回归函数的表达式代表性就很差。
3、简单线性回归方程的建立
建立简单直线回归方程的步骤为:
①设所求的直线回归方程为

学习时,要注意公式中各部分所代表的含义。a是直线的起点,数学上称为纵轴截距;X代表自变量及其变量值;
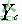
代表因变量的估计值,b表示自变量每增加一个单位时,因变量的平均增加值,在数学上称为直线的斜率,也叫回归系数。
②建立标准方程组,求解方程式中的参数a和b
③把求出的参数a和b的数值代回所设的方程中,即可得所求的方程,然后可用自变量的变化值推算因变量的估计值。
4、估计标准误差分析估计标准误差是衡量因变量的估计值与观测值/考*试*大/之间的平均误差大小的指标。利用此指标可以说明回归方程的代表性。
上一页 [1] [2]
责任编辑:xiaohan

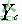 代表因变量的估计值,b表示自变量每增加一个单位时,因变量的平均增加值,在数学上称为直线的斜率,也叫回归系数。
代表因变量的估计值,b表示自变量每增加一个单位时,因变量的平均增加值,在数学上称为直线的斜率,也叫回归系数。