试题一(25分)
阅读下列关于程序测试计划的叙述,在答题纸上回答问题1至问题4。
某程序P包括A~H八个模块,其结构如图1-1所示,其中模块D与G需要调用公共模块E。
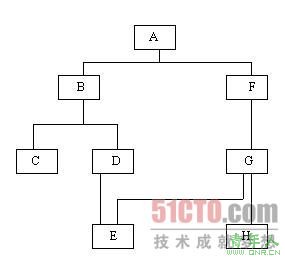 |
| 图1-1 |
现计划采用自顶向下方法执行程序P的测试项目,该项目包括多个作业。设作业A的任务是对模块A进行测试,作业B的任务是对模块B进行测试,…,依此类推。作业P的任务是对程序P进行整体测试。表1-1列出了该项目各作业计划所需的天数、至少必须的天数(即再增大花费也不能缩短的天数)以及每缩短1天测试所需增加的费用。
表1-1
|
作业 |
计划所需天数 |
至少必须的天数 |
每缩短1天所需 增加的费用(元) |
|
A |
2 |
1 |
500 |
|
B |
5 |
3 |
1000 |
|
C |
7 |
4 |
2500 |
|
D |
4 |
3 |
2000 |
|
E |
4 |
2 |
2000 |
|
F |
3 |
2 |
1500 |
|
G |
5 |
4 |
2500 |
|
H |
4 |
2 |
2000 |
|
P |
5 |
5 |
|
图1-2是尚未完成的该项目计划图,其中,每条箭线表示一个测试作业,箭线上标注的字母表示作业名,数字表示计划测试天数。
 |
| (点击查看大图)图1-2 |
【问题1】
请通过填补箭线完成图1-2所示的该项目计划图。若为虚作业,请画成虚箭线;若为实箭线,请在箭线上注明作业名以及计划测试天数。
【问题2】
完成该测试项目计划需要多少天?
【问题3】
(1)如果要求该测试项目比原计划提前1天完成,则至少应增加多少费用,应将哪些测试作业缩短1天?
(2)如果要求该测试项目在(1)的基础上再提前1天完成,则至少应再增加多少费用,应再将哪些测试作业缩短1天?
【问题4】
假设该测试项目已按原计划部署,到了第7天末,发现模块A与B已按计划测试完成,但模块F却刚测试完,比原计划延迟了2天。为了保证该项目仍能在原计划总天数内完成,则至少应增加多少费用,应缩短哪些作业多少天?
试题一分析
该题是网络计划图技术在程序测试项目管理方面的应用。
【问题1】
根据自上而下测试方法,作业F的后续作业是G,因此在计划图上,从节点3到节点4应补箭线,并标注"G,5"。
作业H是作业G的后续作业,而且是作业P(对程序P进行整体测试)的前导作业,因此从节点4到节点6应补箭线,并标注"H,4"。
由于模块E是模块D与G的公共调用模块,按自上而下原则,作业E应紧随作业D与G之后,所以,从节点4到节点5应有虚线箭头,表示虚作业(无需实际工作,只表示时间上的先后顺序),在箭线上不需要标注其他信息。
【问题2】
从节点0到节点7有多条路径,时间总和最长的路径是0-1-2-5-6-7,这就是关键路径,决定了整个项目所需的时间,总共需要的天数为2+5+4+4+5=20天。
【问题3】
为了提前完成项目,必须在关键路径上缩短某些作业的时间。为了节省成本,应选择增加费用最少的作业,缩短其时间。由于缩短某作业的时间后,可能引起关键路径的变化,所以缩短多天的做法需要一次次逐步仔细考虑。
在原计划基础上,为缩短项目1天,应在关键路径上,选择最省钱(增加费用最少)的作业,缩短1天。根据题中给出的表,应选择作业A缩短其1天,增加费用500元。这样做后,关键路径尚没有变化,但作业A已经不能再缩短了。
在此基础上,为再缩短该项目1天,应选择作业B,缩短其1天,增加费用1000元。注意此时,以下三条路径都是关键路径:0-1-2-5-6-7,0-1-3-4-6-7,0-1-3-4-5-6-7。
【问题4】
在作业F延迟两天的情况下,沿路径0-1-3-4-5-6-7以及0-1-3-4-6-7所需的天数均为:
2+5+5+4+5=21天
为了能按原计划20天完成任务,应将这两条路径均压缩1天。
注意作业P是不能压缩的(至少需要5天)。
若单独将作业H压缩1天(需要增加2000元),还不能达到目的。因为路径0-1-3-4-5-6-7仍需要21天。若再将作业E压缩1天(需要增加2000元),则可以按原计划完成项目,但需要增加的费用共4000元。
若单独将作业G压缩1天(需要增加费用2500元),则这两条路径均缩短了1天,可以按原计划完成任务。
从节省费用看,应增加2500元,将作业G压缩1天。
解答要点
【问题1】
 |
(注意:节点4到5为虚箭线)
【问题2】
20天
【问题3】
(1)将作业A缩短1天,需要增加500元
(2)再将作业B缩短1天,需要再增加1000元
【问题4】
应增加2500元,将作业G缩短1天
责任编辑:小草