试题一至试题三是必答题
试题一(共 15 分)
阅读以下说明和算法,完善算法并回答问题,将解答写在答题纸的对应栏内。
[说明]
假设以二维数组 G[1..m,1..n]表示一幅图像各像素的颜色,则 G[i,j]表示区域中 点(i,j)处的颜色,颜色值为 0 到 k 的整数。
下面的算法将指定点(i0,j0)所在的同色邻接区域的颜色置换为给定的颜色值。约定 所有与点(i0,j0)同色的上、下、左、右可连通的点组成同色邻接区域。
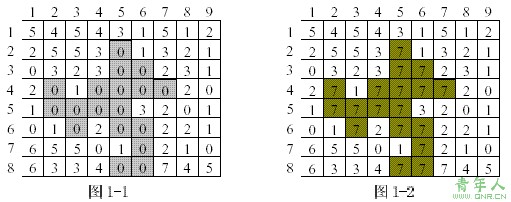
例如,一幅 8×9 像素的图像如图 1-1 所示。设用户指定点(3,5),其颜色值为 0,此时其上方 (2,5)、下方 (4,5)、右方 (3,6)邻接点的颜色值都为 0,因此这些点属于 点(3,5)所在的同色邻接区域,再从上、下、左、右四个方向进行扩展,可得出该同色 邻接区域的其他点(见图 1-1 中的阴影部分)。将上述同色区域的颜色替换为颜色值 7 所得的新图像如图 1-2 所示。
[算法]
输入:矩阵 G,点的坐标(i0,j0),新颜色值 newcolor。
输出:点(i0,j0)所在同色邻接区域的颜色置换为 newcolor 之后的矩阵 G。
算法步骤(为规范算法,规定该算法只在第七步后结束):
第一步:若点(i0,j0)的颜色值与新颜色值 newcolor 相同,则 (1) ;
第二步:点(i0,j0)的颜色值→oldcolor;创建栈 S,并将点坐标(i0,j0)入栈;
第三步:若 (2) ,则转第七步;
第四步:栈顶元素出栈→(x,y),并 (3) ;
第五步:1) 若点(x,y-1)在图像中且 G[x,y-1]等于 oldcolor,则(x,y-1)入栈 S;
2) 若点(x,y+1)在图像中且 G[x,y+1]等于 oldcolor,则(x,y+1)入栈 S;
3) 若点(x-1,y)在图像中且 G[x-1,y]等于 oldcolor,则(x-1,y)入栈 S;
4) 若点(x+1,y)在图像中且 G[x+1,y]等于 oldcolor,则(x+1,y)入栈 S;
第六步:转 (4) ;
第七步:算法结束。
[问题]
是否可以将算法中的栈换成队列?回答: (5) 。
试题二(共 15 分)
阅读以下说明和 C 函数,将应填入 (n) 处的字句写在答题纸的对应栏内。
[说明]
某单位准备进行一次选举,对指定的 n 名(n<80)候选人进行投票。为了简化选举工 作,事先印制了写有这 n 名候选人姓名的选票,投票者只需将选中者名下的圆圈涂黑即可。规定每张选票上被涂黑的圆圈数不得超过 3 个,也不得少于 1 个,否则视为无效选票。投票结束后,所有选票经计算机扫描处理,形成了描述选票状态的文本文件。例如,n=8 时所形成的文件如下:
01011000
10010100
10011000
11111111
00000000
00111000
…
其中,每行表示一张选票的数据,每列代表一位候选者的得票情况。第 i 行第 j 列 为 1,表示第 i 张选票上投了第 j 名候选人 1 票。
函数 statistic( )的功能是读入选票数据,并统计每位候选者的得票数,函数返回 有效选票数。
[C 函数]
int statistic(FILE *fp,int candidate[],int n)
{ /* 从文件中读入选票数据,n 为候选人数量(n<80),从有效选票中统计每位候选者的得票数并存入 candidate[],函数返回有效选票数*/
char str[80]; /* str 保存读入的一张选票数据 */
int i,tag = 0; /* tag 用于判断每张选票是否有效 */
int q = 0; /* q 用于计算有效选票数 */
for(i = 0; i < n; i++)
candidate[i] = 0;
while ( (1) ) {
fgets(str,80,fp); /* 读入一张选票数据 */
for(tag = 0,i = 0; (2) ; i++)
if (str[i] == '1') tag++;
if ( (3) ){ /* 若是有效选票,则进行统计 */
(4) ;
for (i = 0; i < n; i++)
if (str[i] == '1') (5) ;
}
}
return q;
} /* statistic */
试题三(共 15 分)
阅读以下说明和 C 函数,将应填入 (n) 处的字句写在答题纸的对应栏内。
[说明]
若一个矩阵中的非零元素数目很少且分布没有规律,则称之为稀疏矩阵。对于 m 行n 列的稀疏矩阵 M,进行转置运算后得到 n 行 m 列的矩阵 MT,如图 3-1 所示。

为了压缩稀疏矩阵的存储空间,用三元组(即元素所在的行号、列号和元素值)表示稀疏矩阵中的一个非零元,再用一维数组逐行存储稀疏矩阵中的所有非零元素(也称为三元组顺序表)。例如,图 3-1 所示的矩阵 M 相应的三元组顺序表如表 3-1 所示,其转置矩阵 MT 的三元组顺序表如表 3-2 所示。
|
表3-1 矩阵M
|
表3-2 M的转置矩阵MT
|
函数 TransposeMatrix(Matrix M)的功能是对用三元组顺序表表示的稀疏矩阵 M 进行转置运算。
对 M 实施转置运算时,为了将 M 中的每个非零元素直接存入其转置矩阵 MT 三元组顺序表的相应位置,需先计算 M 中每一列非零元素的数目(即 MT 中每一行非零元素的 数目),并记录在向量 num 中;然后根据以下关系,计算出矩阵 M 中每列的第一个非零元素在转置矩阵 MT 三元组顺序表中的位置:
cpot[0] = 0
cpot[j] = cpot[j-1] + num[j-1] /* j 为列号 */
类型 ElemType、Triple 和 Matrix 定义如下:
typedef int ElemType;
typedef struct { /* 三元组类型 */
int r,c; /* 矩阵元素的行号、列号 */
ElemType e; /* 矩阵元素的值*/
}Triple;
typedef struct { /* 矩阵的三元组顺序表存储结构 */
int rows,cols,elements; /* 矩阵的行数、列数和非零元素数目 */
Triple data[MAXSIZE];
} Matrix;
[C 函数]
int TransposeMatrix(Matrix M)
{
int j,q,t;
int *num, *cpot;
Matrix MT; /* MT 是 M 的转置矩阵 */
num = (int *)malloc(M.cols*sizeof(int));
cpot = (int *)malloc(M.cols*sizeof(int));
if (!num || !cpot)
return ERROR;
MT.rows = (1) ; /* 设置转置矩阵 MT 行数、列数和非零元数目 */
MT.cols = (2) ;
MT.elements = M.elements;
if (M.elements > 0) {
for(q = 0; q < M.cols; q++)
num[q] = 0;
for(t = 0; t < M.elements; ++t) /* 计算矩阵 M 中每一列非零元素数目 */
num[M.data[t].c]++;
/* 计算矩阵 M 中每列第一个非零元素在其转置矩阵三元组顺序表中的位置 */
(3) ;
for(j = 1;j < M.cols; j++)
cpot[j] = (4) ;
/* 以下代码完成转置矩阵 MT 三元组顺序表元素的设置 */
for(t = 0; t < M.elements;t++){
j = (5) ; /* 取矩阵 M 的一个非零元素的列号存入 j */
/* q 为该非零元素在转置矩阵 MT 三元组顺序表中的位置(下标)*/
q = cpot[j];
MT.data[q].r = M.data[t].c;
MT.data[q].c = M.data[t].r;
MT.data[q].e = M.data[t].e;
++cpot[j]; /* 计算 M 中第 j 列的下一个非零元素的目的位置 */
} /* for */
} /* if */
free(num); free(cpot);
/*此处输出矩阵元素,代码省略*/
return OK;
} /* TransposeMatrix */
责任编辑:小草